EJERCICIOS MOVIMIENTO CIRCULAR

Estimados estudiantes, en esta semana vamos a aplicar la teoria estudiada en semanas anteriores y resolver ejercicios de la siguiente página para ver click aqui.  del numeral 1 al numeral 10.

Aqui un video de ejemplo de como deben realizar los ejercicios.

para ver el video video click aqui

VIDEOS SOBRE MOVIMIENTO CIRCULAR

VER LOS VIDEOS Y HACER MAPAS CONCEPTUALES

GRADOS Y RADIANES.

DESPLAZAMIENTO ANGULAR, VELOCIDAD ANGULAR Y ACELERACION ANGULAR

CALCULO DE LA LONGITUD DE ARCO.

VELOCIDAD ANGULAR PERIODO Y FRECUENCIA

FUNDAMENTOS DE MOVIMIENTO CIRCULAR

En esta semana vamos a repasar los conceptos fundamentales, acerca de movimiento circular, en forma general:

 

Como tarea realizar los mapas conceptuales de este tema que consta en el libro de texto.

MOVIMIENTO CIRCULAR

El movimiento circular es el que recorre una partícula o cuerpo por una circunferencia. Este movimiento tiene un eje y todos los puntos por los que pasa la partícula se encuentran a una distancia constante (r) del eje.

Existen diferentes variables o conceptos muy importantes para explicar el movimiento circular:

• Eje: punto fijo en el centro de la circunferencia por la que gira el cuerpo.
• Radio: distancia a la que gira el punto P sobre el eje O (en nuestro caso r).
• Posición: punto P en el que se encuentra la partícula.
• Posición angular: es el ángulo (𝚹) que forma la partícula con respecto al eje x
• Velocidad angular: define la variación angular por unidad de tiempo (ω)
• Velocidad tangencial: es el módulo de la velocidad en cualquier punto del giro y viene definido como el recorrido, en unidades de longitud, que describe P por unidad de tiempo (v_t).
• Aceleración angular: es el incremento de velocidad angular por unidad de tiempo (α).
• Aceleración tangencial: se define como el incremento de velocidad lineal por unidad de tiempo (a_t).
• Aceleración centrípeta: componente que va dirigida hacia el centro de la circunferencia. Representa el cambio de dirección del vector velocidad (a_cen).
• Período: tiempo T que tarda la partícula en dar una vuelta al círculo.
• Frecuencia: número de vueltas f que recorre la partícula en una unidad de tiempo. Se expresa en ciclos/seg o hertzios.

Movimiento circular uniforme	Movimiento en círculo con rapidez constante.
Radián	La razón de la longitud de un arco a su radio. Existen $2\pi$2, pi radianes en un círculo de $360 \degree$360, degree o una revolución. Adimensional.
Velocidad angular ($\omega$omega)	Medida de cómo un ángulo cambia con el tiempo. El análogo rotacional de la velocidad lineal. Cantidad vectorial en la que el sentido contrario a las manecillas del reloj se define como la dirección positiva. En el Si tiene unidades de $\dfrac{\text{radianes}}{\text {s}}$start fraction, start text, r, a, d, i, a, n, e, s, end text, divided by, start text, s, end text, end fraction.
Aceleración centrípeta ($a_c$a, start subscript, c, end subscript)	La aceleración apunta hacia el centro de una trayectoria curva y es perpendicular a la velocidad del objeto. Hace que un objeto cambie su dirección y no su rapidez a lo largo de una trayectoria circular. También se llama aceleración radial. En el SI tiene unidades de $\dfrac{\text m}{\text s^2}$start fraction, start text, m, end text, divided by, start text, s, end text, squared, end fraction.
Periodo ($T$T)	Tiempo necesario para una revolución. Inversamente proporcional a la frecuencia. En el SI tiene unidades de $\text{s}$start text, s, end text.
Frecuencia ($f$f)	Número de revoluciones por segundo para un objeto giratorio. En e SI sus unidades son $\dfrac{1}{\text{s}}$start fraction, 1, divided by, start text, s, end text, end fraction o $\text{Hertz (Hz)}$start text, H, e, r, t, z, space, left parenthesis, H, z, right parenthesis, end text.

Ecuaciones

Ecuación	Significado de los símbolos	Significado en palabras
$\Delta \theta = \dfrac{\Delta s}{r}$delta, theta, equals, start fraction, delta, s, divided by, r, end fraction	$\Delta \theta$delta, theta es el ángulo de rotación, $\Delta s$delta, s es la distancia recorrida alrededor de un círculo y $r$r es el radio.	El cambio en el ángulo (en radianes) es la relación de la distancia recorrida alrededor del círculo con el radio del círculo.
$\bar \omega = \dfrac{\Delta\theta}{\Delta t}$omega, with, \bar, on top, equals, start fraction, delta, theta, divided by, delta, t, end fraction	$\bar \omega$omega, with, \bar, on top es la velocidad angular promedio, $\Delta\theta$delta, theta es el ángulo de rotación y $\Delta t$delta, t es el cambio en el tiempo.	La velocidad angular promedio es proporcional al desplazamiento angular e inversamente proporcional al tiempo.
$v = r \omega$v, equals, r, omega	$v$v es la velocidad lineal, $r$r es el radio, $\omega$omega es la velocidad angular.	La velocidad lineal es proporcional a la velocidad angular por el radio $r$r.
$T = \dfrac{2\pi}{\omega} = \dfrac{1}{f}$T, equals, start fraction, 2, pi, divided by, omega, end fraction, equals, start fraction, 1, divided by, f, end fraction	$T$T es el periodo, $\omega$omega es la velocidad angular y $f$f es la frecuencia.	El periodo es inversamente proporcional a la velocidad angular multiplicado por un factor de $2\pi$2, pi e inversamente proporcional a la frecuencia.

Cómo relacionar al velocidad lineal y la velocidad angular

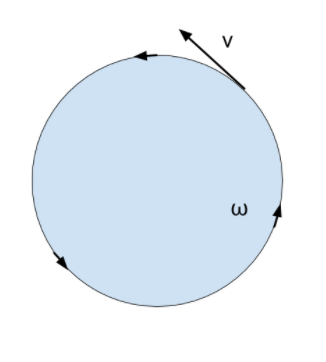
La velocidad angular $\omega$omega es el desplazamiento angular dividido entre el tiempo, mientras que la velocidad (lineal) $v$v es el desplazamiento lineal dividido entre el tiempo (Figura 1). A veces a la velocidad lineal también se le llama velocidad tangencial.

Figura 1. Velocidad angular contra velocidad lineal

La velocidad angular no cambia con el radio

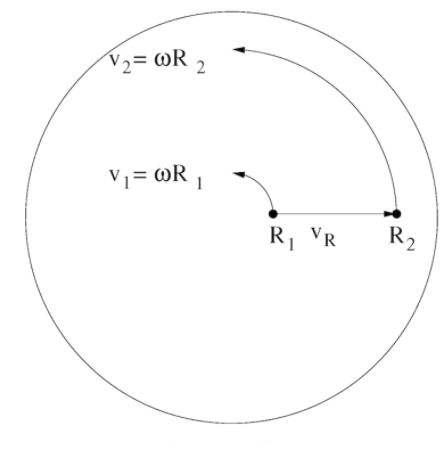
La velocidad angular no cambia con el radio, pero sí lo hace la velocidad lineal. Por ejemplo, en una banda que marcha y dobla una esquina, la persona que está afuera debe dar pasos más grandes para mantenerse en línea con todos los demás. Por lo tanto, la persona que está al exterior tiene una velocidad lineal mucho mayor que la persona más al interior. Sin embargo, la velocidad angular de cada persona en la línea es la misma porque se mueven el mismo ángulo en el mismo tiempo (Figura 2).

Figura 2. La velocidad angular sigue siendo la misma independientemente de la distancia desde el centro, pero la velocidad lineal aumenta proporcionalmente con el radio. Imagen adaptada de Wikimedia